Quantum Tunneling in Gradual Potentials
DOI:
https://doi.org/10.37636/recit.v225057Keywords:
Tunnel effect, Quantum tunneling, Smooth barriers.Abstract
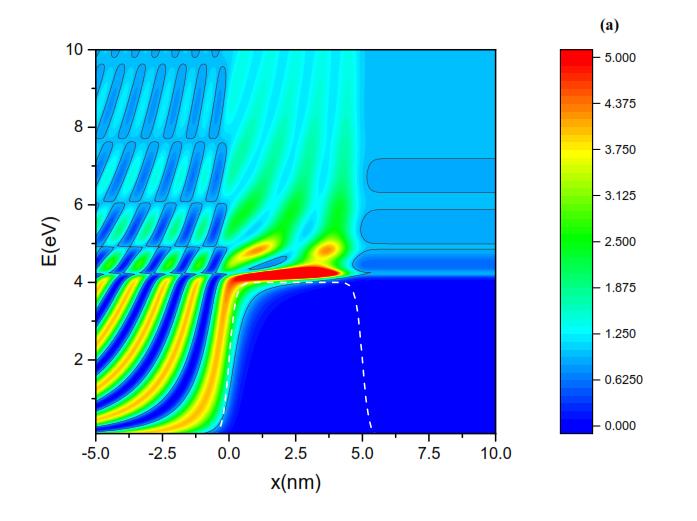
One of the paradigmatic phenomena of quantum mechanics is undoubtedly the so-called tunnel effect, which manifests itself as the possibility of particles on the nanometer scale to traverse potential barriers. This phenomenon, although unintuitive, is so real that it plays a prominent role in current technology and constitutes the key mechanism of electronic transport in novel concepts of nanoelectronic devices. In this work, maps of electron density are used to illustrate the spatial and energetic distribution of electrons that propagates through gradual potential barriers, visualizing the wave nature of the electrons and the tunneling phenomenon. In particular, the effect of using gradual barriers rather than rectangular barriers is discussed.Downloads
References
R. Waser. Nanoelectronics and Information Technology. 2005 WYLEY-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany. https://www.wiley.com/en-us/Nanoelectronics+and+Information+Technology%3A+Advanced+Electronic+Materials+and+Novel+Devices%2C+3rd+Edition-p-9783527409273
L. Esaki and R. Tsu, "Superlaticce and negative differential conductivity in semiconductors," IBM J. Res. Develop. vol. 14, pp. 61-65, 1970. https://doi.org/10.1147/rd.141.0061 DOI: https://doi.org/10.1147/rd.141.0061
R. Tsu and L. Esaki. 1973. "Tunneling in a finite superlattice," Appl. Phys. Lett, vol. 22, pp. 562, 1973. https://doi.org/10.1063/1.1654509 DOI: https://doi.org/10.1063/1.1654509
J. M. Chamberlain, L. Eaves and J.C. Portal, Electron Properties of Multilayers and Low-Dimensional Semiconductor Structures. NY: Ed. Plenum Press, 1990, L. Esaki, The evolution of semiconductor quantum structures in reduced dimensionality. Do-it -yourself quantum mechanics, pp. 124. https://arxiv.org/pdf/1007.5386
D. K. Ferry, S. M. Goodnick and J. Bird. Transport in nanostructures. New York, NY, USA: Cambrige University Press, 1997, pp. 91-121. https://doi.org/10.1017/CBO9780511840463 DOI: https://doi.org/10.1017/CBO9780511840463
C. Weisbuch and B. Vinter. Quantum Semiconductor Structures:Fundamentals and Applications. Inc. San Diego, California, USA: Academic Press, 1991, pp. 189-215.
https://doi.org/10.1016/B978-0-08-051557-1.50010-X DOI: https://doi.org/10.1016/B978-0-08-051557-1.50010-X
S. Mandrà, S. Valleau and M. Ceotto. "Deep Nuclear Resonant Tunneling Thermal Rate Constant Calculations," Int. J. Quantum Chem. J., vol. 113, pp. 1722-1734, 2013. https://doi.org/10.1002/qua.24395. DOI: https://doi.org/10.1002/qua.24395
C. Grossert, M. Leder, S. Denisov, P. Hänggi, and M. Weitz, “Experimental control of transport resonances in a coherent quantum rocking ratchet,” Nat. Commun., vol. 7, no. 1, p. 10440, 2016. https://doi.org/10.1038/ncomms10440 DOI: https://doi.org/10.1038/ncomms10440
T.J. Slight and C.N. Ironside. "Investigation into the Integration of a Resonant Tunnelling Diode and an Optical Communications Laser: Model and Experiment". IEEE J. of Quantum Electron., vol. 43, no. 7, pp. 580, 2007. https://doi.org/10.1109/JQE.2007.898847 DOI: https://doi.org/10.1109/JQE.2007.898847
Downloads
Published
Issue
Section
Categories
License
Copyright (c) 2019 Cristian Gabriel Herbert Galarza, Rogelio Orozco Duarte, Roberto Romo Martínez

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors who publish in this journal accept the following conditions:
The authors retain the copyright and assign to the journal the right of the first publication, with the work registered with the Creative Commons Attribution license 4.0, which allows third parties to use what is published as long as they mention the authorship of the work and the first publication in this magazine.
Authors may make other independent and additional contractual agreements for the non-exclusive distribution of the version of the article published in this journal (eg, include it in an institutional repository or publish it in a book) as long as they clearly indicate that the work it was first published in this magazine.
Authors are allowed and encouraged to share their work online (for example: in institutional repositories or personal web pages) before and during the manuscript submission process, as it can lead to productive exchanges, greater and more quick citation of published work (see The Effect of Open Access).











