Numerical analysis of the dispersion of a contaminant through a simplified porous medium
DOI:
https://doi.org/10.37636/recit.v428798Keywords:
Porous media, Turbulent flow, Pollutan dispersionAbstract
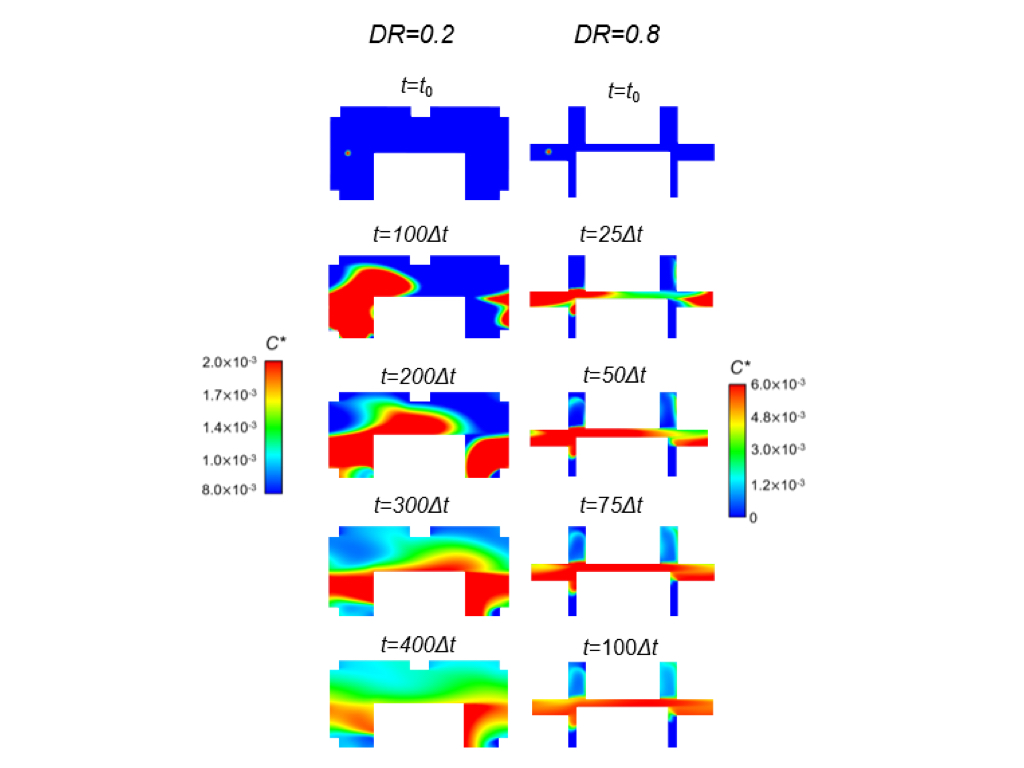
It is presented the numerical analysis of the pollutant dispersion in porous media composed of infinite arrays of particles with different diameter ratios (DR). The DR ranged from 0.2 to 0.8, representing several degrees of expansion-contraction of the pore paths, not included in previous models. The corresponding porosities (f) covered the interval 0.27<f<0.72, and the pore Reynolds number was set to 50×103 which represented fully developed turbulent conditions. Results showed that for the case of DR=0.2 and f=0.27, the wake structures behind the smaller particles are elongated along with the gap spaces between particles, enhancing hence, the tracer dispersion. Oppositely, for the highest DR case, the porosity is lower and although the local velocities are high, the wake behind smaller particles are disrupted, and the homogeneity time increased drastically. Thus, eddy structures inside pore domains play a key role in the dispersion of a tracer. Taking into account that domains with large f contain less solid phase, this effect could be considered in the optimization of several engineering devices as cooling fins, arrays of tubes in heat exchangers, and static mixers to mention a few.
Downloads
References
A. Dybbs and R. V. Edwards, Fundamentals of Transport Phenomena in Porous Media. 1984.
J. S. Weitzman, L. C. Samuel, A. E. Craig, R. B. Zeller, and S. G. Monismith, "On the use of refractive ‑ index ‑ matched hydrogel for fluid velocity measurement within and around geometrically complex solid obstructions," Exp. Fluids, vol. 55, no. November, pp. 1-12, 2014. DOI: https://doi.org/10.1007/s00348-014-1862-x
https://doi.org/10.1007/s00348-014-1862-x. DOI: https://doi.org/10.1007/s00348-014-1862-x
Y. Jin, M. F. Uth, A. V. Kuznetsov, and H. Herwig, "Numerical investigation of the possibility of macroscopic turbulence in porous media: A direct numerical simulation study," J. Fluid Mech., vol. 766, pp. 76-103, 2015. https://doi.org/10.1017/jfm.2015.9. DOI: https://doi.org/10.1017/jfm.2015.9
A. Rasam, G. Brethouwer, P. Schlatter, Q. Li, and A. V. Johansson, "Effects of modelling, resolution and anisotropy of subgrid-scales on large eddy simulations of channel flow," J. Turbul., vol. 12, no. December, pp. 1-20, 2011. https://doi.org/10.1080/14685248.2010.541920 DOI: https://doi.org/10.1080/14685248.2010.541920
C. Hrenya, S. Miller, T. Mallo, and J. Sinclair, "Comparison of low Reynolds number k-ε turbulence models in predicting heat transfer rates for pipe flow," Int. J. Heat Mass Transf., vol. 41, no. 11, pp. 1543-1547, 1998. https://doi.org/10.1016/S0017-9310(97)00208-1. DOI: https://doi.org/10.1016/S0017-9310(97)00208-1
F. Kuwahara, T. Yamane, and A. Nakayama, "Large eddy simulation of turbulent flow in porous media," Int. Commun. Heat Mass Transf., vol. 33, no. 4, pp. 411-418, 2006. https://doi.org/10.1016/j.icheatmasstransfer.2005.12.011. DOI: https://doi.org/10.1016/j.icheatmasstransfer.2005.12.011
P. Kundu, V. Kumar, Y. Hoarau, and I. M. Mishra, "Numerical simulation and analysis of fluid flow hydrodynamics through a structured array of circular cylinders forming porous medium," Appl. Math. Model., vol. 40, no. 23-24, pp. 9848-9871, 2016. https://doi.org/10.1016/j.apm.2016.06.043. DOI: https://doi.org/10.1016/j.apm.2016.06.043
J. Tu, G.-H. Yeoh, and C. Liu, Computational Fluid Dynamics, A Practical Approach, Second. Massachusetts: Butterworth-Heinemann, 2009.
D. C. Wilcox, Turbulence Modeling for CFD, First ed. California: DCW Industries, 1993.
M. H. J. Pedras and M. J. S. de Lemos, "Macroscopic turbulence modeling for incompressible flow through undefromable porous media," Int. J. Heat Mass Transf., vol. 44, no. 6, pp. 1081-1093, 2001. https://doi.org/10.1016/S0017-9310(00)00202-7. DOI: https://doi.org/10.1016/S0017-9310(00)00202-7
A. Nakayama and F. Kuwahara, "A macroscopic turbulence model for flow in a porous medium," J. Fluids Eng., vol. 121, no. June 1999, pp. 427-433, 1999. https://doi.org/10.1115/1.2822227. DOI: https://doi.org/10.1115/1.2822227
A. Nakayama and F. Kuwahara, "A General Macroscopic Turbulence Model for Flows in Packed Beds, Channels, Pipes, and Rod Bundles," J. Fluids Eng., vol. 130, no. 10, p. 101205, 2008. https://doi.org/10.1115/1.2969461. DOI: https://doi.org/10.1115/1.2969461
J. Yang, M. Zhou, S. Y. Li, S. S. Bu, and Q. W. Wang, "Three-dimensional numerical analysis of turbulent flow in porous media formed by periodic arrays of cubic, spherical, or ellipsoidal particles," J. Fluids Eng. Trans. ASME, vol. 136, no. 1, p. 011102, 2014. https://doi.org/10.1115/1.4025365. DOI: https://doi.org/10.1115/1.4025365
A. Alonzo-Garcia, A. T. Mendoza-Rosas, M. A. Díaz-Viera, S. A. Martinez-Delgadillo, and E. Martinez-Mendoza, "Assessment of Low-Re turbulence models and analysis of turbulent flow in porous media consisting of square cylinders with different diameter ratios," J. Fluids Eng., vol. 143, no. 1, p. 18, 2020. https://doi.org/10.1115/1.4048284. DOI: https://doi.org/10.1115/1.4048284
Downloads
Published
License
Copyright (c) 2021 Lucía Morales Arévalo, Dr. René San Juan Galindo, Dra. Norma Alicia Ramos Delgado, Dr. Oscar Adrián Morales Contreras, Dra. Ana Teresa Mendoza Rosas, Dr. Alejandro Alonzo García

This work is licensed under a Creative Commons Attribution 4.0 International License.
The authors who publish in this journal accept the following conditions:
The authors retain the copyright and assign to the journal the right of the first publication, with the work registered with the Creative Commons Attribution license 4.0, which allows third parties to use what is published as long as they mention the authorship of the work and the first publication in this magazine.
Authors may make other independent and additional contractual agreements for the non-exclusive distribution of the version of the article published in this journal (eg, include it in an institutional repository or publish it in a book) as long as they clearly indicate that the work it was first published in this magazine.
Authors are allowed and encouraged to share their work online (for example: in institutional repositories or personal web pages) before and during the manuscript submission process, as it can lead to productive exchanges, greater and more quick citation of published work (see The Effect of Open Access).











